|
3D Geometry Primer: Chapter 1 - Issue 10 - Addendum: What I Didn't Tell You (Yet) by (16 October 2000) |
Return to The Archives |
Addendum: What I Didn't Tell You (Yet)
 |
|
Right, this really is the last issue of the 1st chapter. I've been telling you this
already for a few issues, but now it's really the end. But don't be mournful, in a
few weeks/months, there will be chapter II :) Today, I'll tell you things I forgot to tell you in the past issues. I'll give you answers to questions that you asked me, and give you answers I've got on questions I've asked. But, let's start with a question of yours, which I will turn into a new question :) |
(I) Why The Dot And Cross Products Are What They Are ...
 |
|
... some people asked. They wondered why the dot product isn't e.g.
U·V = ||U||*||V||*sin(theta) instead of
||U||·||V||*cos(theta). Let us be clear: the definition
with the sin(theta) is a wrong one. This was a very good question, since I didn't know the answer myself. So, in a mail to Max McGuire, I asked if he did know this. He answered (in which I can agree) that the reason probably is, that someone needed someday an operator that did that right thing. So, he invented the dot or cross product. And that operator turned out to be that handy, that it's used by everybody now for anything now. Unfortunately, we don't know in what situations those products came into being. We think that the orthogonal (= perpendicular) projection has something to do with the "invention" of the dot product, but we don't know exactly how. So, I someone has any ideas about this, here's my address. We'd be very happy to know it ... Editor's Note: Bram started up a thread on flipCode's forums regarding this issue. Do be sure to check it out here, hopefully where you will share your knowledge on the subject: Origin of Dot/Cross Products |
(II) Areas Of Triangles And Volumes Of Tetrahedras
 |
|
a) Areas Of Triangles How do you compute the area of a triangle? Well, I hope you remember the following picture: the area of the triangle ABC is exactly the half of the parallellogram ABDC: a = (b*h)/2 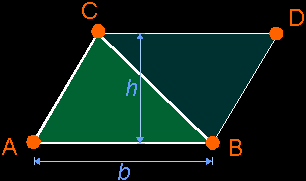 But then, of course, you must know the base b and height h of the triangle, which isn't always that easy if you just have the coordinates of the vertices A, B and C. But here comes the trick: if you take the magnitude of the cross product (AB)×(AC), then you become exactly the area of the parallelogram enclosed between the vectors AB and AC. So, if you take the half of it, you become the area of you triangle ABC. 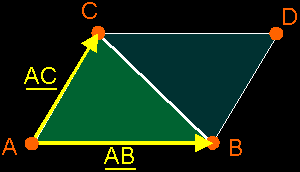 Area a of triangle ABC = (1/2)*||(B–A)×(C–A)|| (Remark: the notation AB is just a way to talk about the free vector that fits between points A and B, which can be calculated by: AB = B – A) b) Volumes of tetrahedras 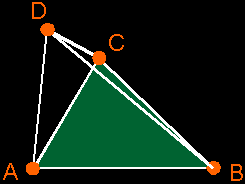 I don't know if you know this, but if you want to calculate the volume v of a pyramid ABCD (which the tetrahedra is), then you take 1/3 of the volume of a prism ABC DEF with the same base surface and height. It's possible to prove this, but that's something with integrals. So, I won't do that here. 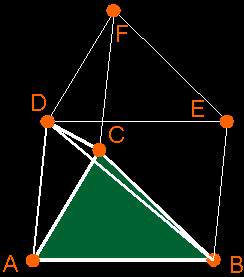 But that prism is also exactly the half of the parallelepiped ABCG DEFH. And the volume of that parallelepiped can be calculated with the triple product (AB AC AD). 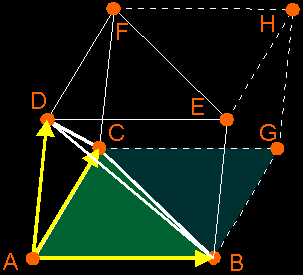 In that way, it's possible to compute the volume of the tetrahedra ABCD by taking 1/6 of the volume of the parallelepiped. Don't forget to take the absolute value of the triple product, since it can be positive or negative. Volume v of tetrahedra ABCD = abs( (1/6)*(AB AC AD) ) = abs( (1/6) * ((B–A)×(C–A))·(D–A) ) |
(III) Why Is The Origin Of The Screen In The Upper-Left Corner?
 |
|
In issue I.05 you could read
this question. I told you how you could use this artifact to your advantage,
but I didn't really answer the question. Since I didn't know the answer myself,
I guess. Some people have mailed me to give that answer, and now I want to give
it to you. Here's the one posted by Paul: I just read your article on flipcode and saw that you are not sure why the origin of the screen is in the upper left-hand corner, so I thought you might like to know the answer. It might surprise you to learn that the reason has nothing to do with 3d-graphics, software, or even computers. The person behind this always annoying problem was an engineer from the 1920's (sorry I forgot his name, but he was a Russian living in the US). He was the person that invented the first television set that used a cathode ray tube and electron gun combination to display pictures on the screen (earlier sets, dating back to the late 19th century had used spinning perforated disks and lamps to display the picture). Anyway all future TVs, and hence computer monitors, used his system for displaying the picture. It just happens that they way he built the thing the electron gun starts scanning in the upper-left hand corner of the screen and then scans from left to right, and top to bottom (I'm going to guess he did this because its the way western people read). So when electrical engineers first started hooking monitors up to computers the origin had already been placed for them by this guy. That's the way it was and they went with it. Now today it's easy to use a little code to move the origin to wherever you want it in software, but at the hardware level the origin is always going to be in the upper-left corner. I hope this helps clear things up. Paul |
(IV) Free Vectors As Linear Combinations Of Points
 |
In the same way as it's possible to set conditions to weight-factors
w[i] in a lin. comb. of points to achieve a new point
(independent to the origin); it's possible to become a free vector as a
lin. comb. of points (also independent to the origin). How? First,
let's write down what we want: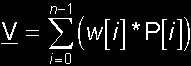 You can use an analogue reasoning as in the last issue to become the condition on w[i], but I'll leave that as an exercise to the reader. Here, I will tell you a more intuitive reasoning: At the right side, you see w[i]*P[i] which you will write as w[i]*OP[i]. This place vector contains the origin O and the point P[i]. This means that for each point P[i] at the right side, you will also have a w[i]*O. If you summate this, you will have a Sw[i]*O at the right side. But at the left side, you only have the already free vector V. No origin O is in there. So, if you want both sides to be equal, then you may not have an origin in the right side too. This is why Sw[i] must be 0 (zero). In one line, this becomes: 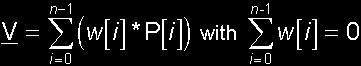 |
(V) Splitting Up Barycentric Combinations
 |
It's always possible to split up a barycentric comb. in a convex barycentric
comb. (in which all w[i]³0) and
a "free vector comb." (in which Sw[i]=0). This is very easy to prove
if you take the barycentrum (w[i]=1/n) as convex
barycentric comb. Then each barycentric combination can be written as the sum
of the barycentrum + a free vector: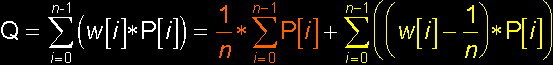 Convince yourself that this is correct. The orange part is the barycentrum (which is convex) and the yellow part is the free vector. In some situations, it's possible to split this combinations in a better way. I'll give you an example. Say, you have the combination Q = (0.5)*A + B – C + (0.5)*D. You can write this as: Q = ((0.5)*A + (0.5)*D) + (B – C), which is the middle of the points A and B *plus* the free vector CB. Now you immediately see what Q will be. I don't know where you can use this, but it shows you that each barycentric combination can be written as the sum of a convex barycentric comb. + a free vector. |
(VI) Clifford Algebra
 |
|
Many many weeks ago, Jaap Suter passed me a link to an algebra site with an
introduction on Clifford Algebra. I said that I would put this link in my
primer one day. I think that, no, I'm sure that, the stuff explained there, will
be very scary for most of you, but hey I've promised Jaap :) So here it is:
Introduction to Geometric Algebra. In fact, I'm
already a few weeks too late, since Tim already posted this in the news
section. This is it. The last word of chapter one ... There's nothing more to say than a 'goodbye', so: "goodbye and CU in chapter II". Regards, Bramz "And what I see, you can not see. That when I move, you move with me" - Ribeiro (Moonspell) |