|
Plücker Coordinates for the Rest of Us - Part 3 by Lionel Brits (15 November 2001) |
Return to The Archives |
Back to Reality
 |
Of course we must also be able to work backwards; that is, we
must be able to find the line, if it exists, that corresponds to a Plücker
coordinate. Given a coordinate  , we
know that  .
Our aim is to find  .In particular, we know that:    After rearranging the above equations, finding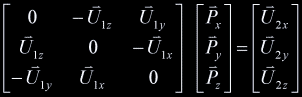
merely involves solving the following system: Since any point on the line would be a solution of this system, we know that the system has infinitely many solutions (it is undetermined), and thus the coefficient matrix has no inverse. We could proceed by row reduction or whatever method. The general solution would to this system would have the form  ,
which is precisely what we are after.An easier way to proceed was pointed out to me by Conor Stokes. The vector 
points from the origin to a point on the line that is closest to the origin.
Recall that .Consider the point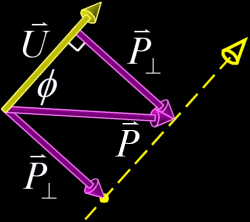 
on the line which is is the point closest to the origin. is
the component of
perpendicular to  .
If 
is the smallest angle between
and ,
then  .
From the definition of the cross-product we can now say  .
Consider now the vector ,
that is, .
Another cross product identity gives us  .
Since
is perpendicular to  ,
we can write: Marvelous! We can now decompose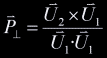
into a direction
and a point  .
|
|
An Alternate Representation
|
We have so far treated the Plücker representation of a line as
a 6D coordinate, ,
with being
the direction of the line and 
being an abstract construct analogous to a torque or moment of the line about
the origin. We can also deal with the individual components of a Plücker
coordinate separately. Since we haven't committed ourselves to any choice of
axes, we can order and direct these components quite arbitrarily. Herein lies an
alternate representation of the equivalent Plücker coordinate ,
namely  .
The following convention is usually adopted:      Or alternatively, given a line from point
to 
:      For this representation the corresponding version of the permuted inner product is:  This representation of the Plücker coordinate corresponds to a hyperplane containing all lines in 3D that intersect the line it represents. Though not a plane in the familiar sense, it is a hyper plane because it divides the Plücker-space into two (lines outside either have CW or CCW relationship with the line the hyper plane represents). This representation of the product has the property that it is zero whenever 
and 
intersect or are parallel, and nonzero otherwise.
|
|
What is it Good For?
|
| Oodles! Go right ahead and find out. |
|
Article Series:
|