flipcode - Basic Collision Detection

Basic Collision Detection
by (21 January 2000)

Introduction

I've seen a few tutorials on basic collision detection around the net, but most of them I've read are either pretty confusing or somewhat incomplete. I've attempted here to write a tutorial that anyone with a basic understanding of 3D concepts and linear algebra should be able to pick up on quickly. If you're already familiar with collision detection, there's no real reason to read further. I'm not presenting anything new here, just stating the basics and suggesting a few possibly "better" ways to do a step or two.

Collision Detection

Lets start with what we're trying to do in the first place. So you've got your engine up and running, but you can walk through walls and things like this. That's not very cool, so you want to detect when your viewer has hit a part of the world and then respond (for example by not letting him move there). That's our goal, and at its simplest, its indeed very simple to achieve. Assume we're talking about a camera that is going to move to position: "destination". To perform basic collision detection, we want do the following:

Determine if "destination" will cross the "plane" of any polygon in the portion of the world we're checking against.
Find out where exactly the intersection would be on that plane and determine if that point of intersection is actually within the boundaries of the polygon.

The good thing is that you move on to the next step if and only if the first step checks out. For example if your "destination" doesn't cross any planes, you don't need to do anything with the intersection point because there is no intersection. This may cut down calculation time quite a bit since your viewer won't be colliding with very many polygons at once.

Now, I won't insult you. If you're ready to add collision detection to your engine that you've already got up and running, I'm assuming you're familiar with planes in 3-space. If you're not too sure about planes and their respective equations, you might want to find some other references. I won't regurgitate the information here. I'm sorry.

Just so we're on the same page, when I speak of planes, I'm talking about a normal vector and scalar distance (taken right from its equation).

To avoid mentioning it later, I am in fact only dealing with convex polygons. For every polygon, be sure you've calculated its plane normal and distance. To do step 1, lets assume you have "position" and "destination". As before, "destination" is where your viewer wants to move to (for example after someone hits the "forward" key) and "position" is where your camera currently is. To determine if your destination will cross a polygon's plane, simply do the following (psuedo code):


  int ClassifyPoint( CPlane3D *plane, CPoint3D *destPt )
  {
        scalar p = DotProduct( plane->normal, destPt ) + plane->distance;

        if( p > 0.0f ) return PLANE_FRONT;
        else
        if( p < 0.0f ) return PLANE_BACK;

        return PLANE_COINCIDE;
  }

For our purposes, PLANE_[type] are just integer constants to distinguish between sides of the plane. It should be obvious now that for each polygon's plane in your data set, you can run ClassifyPoint with "position" and again with "destination". If they return different values from each other, you've run into (or passed) a polygon's plane. This means the point where your camera is, and the point where your camera wants to move to, are not on the same side of the plane you're checking. Take a moment to visualize that if you're not following so far. That's at the very heart of collision detection.

Now, this does not mean you've collided with a polygon. It just means your destination would pass a polygon's plane. Remember that a hyperplane is infinite, so just because you've crossed the plane, doesn't mean you're within the finite boundaries of the actual polygon which is "lying on" the plane. Now we need to check if it actually hit the polygon. That's where the next step come in.

Next up, we need to find the intersection point. This isn't a very difficult task. You have the start and end points of a "line" in 3-space (your "position" and "destination"), so subtract the start (position) from the end (destination) to get a direction vector that we'll call "ray". ray = destination minus position. Now, remember your linear algebra. A line in 3-space can be defined as follows:


  lx = start.x + (ray.x * t)
  ly = start.y + (ray.y * t)
  lz = start.z + (ray.z * t)

Where substituting a value for t will get you any point along the line. See the connection? Since we want to figure out what t is, given everything else, we simply need to plug all of this into the plane's equation, which we can simplify into dot products and end up with the following:


  t = - ( DotProduct( plane->normal, start) + plane->distance )   /
          DotProduct( plane->normal, ray)
        
  CPoint3D intersect = start + (ray * t);

One quick word of warning. You should actually check the denominator when calculating t above. If its zero, you of course don't want to divide by zero, but that would also indicate that the normal and the ray are orthogonal. Visualize that (remember that the normal is orthogonal to the plane we're working with) and you will realize that there won't be any single unique intersection point to work with, and thus we can't continue. But assuming the denominator isn't zero, we should now have the intersection point, which is where the viewer collided with the plane.

There's one final thing to do which is to check if this intersection point is actually ON the polygon, within its boundaries (not just on its infinite plane). Remember, we're talking convex polygons only (ha! I repeated it anyway)!

This last step is actually one that can be done many ways. Keep in mind that at this point, we KNOW the point is on the plane, and we even know exactly where. That's important. Here are a few ways to check if the point is on the polygon:

One method to do the test is to create a plane for each edge of the polygon, with their normals all pointing in (ie, towards the center of the polygon) or out. Then you would run ClassifyPoint for the point in question with each of these new planes. If all of the points were on the "inside", that means the point is within the polygon's boundaries. That will work, but I'd rather not do so much work.

Another method, which even works for polygons that aren't neccesarily convex, can be found on the web pages of Paul Bourke. This document, explains a method for determining if a point lies within the boundaries of a 2D polygon. I haven't tried this one.

Another idea, which I first read about in a book called "3D Game Programming With C++", is pretty simple. Take a look at the following image: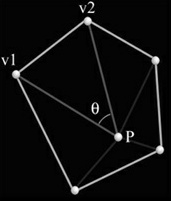

If you take a convex polygon such as the one shown here, and if your point P (our intersection point) is in fact on the polygon, you'll notice that the sum of the angles formed by creating vectors from P to each pair of vertices in order as you travel "around" the polygon, will in fact equal 2pi radians, also known as 360 degrees. Calculate theta for the triangle formed by vectors made from each sequential pair of verts and P, and then add them to the current sum. If it equals 2pi (or is very close... keep in mind variable precision), then you can consider the point on the polygon. Calculating the angles is very easy if you remember your linear algebra. Think about the definition of the dot product and you'll realize that the angle can be worked out by normalizing the 2 vectors (from p to 2 vertices), and taking the inverse cosine of the dot product between those vectors.

The result is in radians, so when you sum up all of the angles, you'll want to check if you end up with 2pi. Note that the vectors do have to be normalized in order to calculate the angles. That's one major drawback of this method (computing the magnitudes), but its not too bad. The other drawback, which I mentioned above is that with floating point precision, this method is NOT ultra-precise. I have tried this in my collision routines, and it does work rather nicely, but if you seek precision (and incredible speed), you'll either need to come up with a clever kludge or consider using another method.

So, what other methods are there to find out if you've hit a polygon? If we're talking triangles, here's a link to a page with source code by Tomas Möller and Ben Trumbore: Fast, Minimum Storage Ray-Triangle Intersection, which presents a method for checking for ray/tri intersections, even without knowing the plane equation. Listed on the page, there's also source code to Badouel's algorithm, which is a fast method if you do have the plane equation (which, I'm guessing you do). Btw, thanks to the various people I've talked to about this and who mentioned these links to me, most notably Hasty. You may also want to check out the Graphics Gems. My point is that there are a lot of ways to run this test, so you just need to pick one that fits what you're doing.

Anyway, after all of this work, if your point in polygon routine returns true, you can now conclude that your viewer's movement would actually cause a collision with this polygon. That's all there is to it! Of course now you have to actually do something about it. This introduces the whole subject of "collision response", which I will not cover in much depth at all. At the very simplest, you can just not change the viewer's "position" to "destination" if a collision is detected. That will cause the viewer to suddenly STOP when he collides with world geometry. This may feel awkward since most of you have probably played games like Quake where you slide along a wall if you collide with it rather than just stopping and manually turning directions. To get a sliding sort of effect, you can push the viewer back in the direction of the polygon's normal by a certain amount. Consider the effect of that. Imagine, for example, the viewer hitting the polygon at a 45 degree angle to the polygon's normal, then being pushed back a little along the normal. You'll still be able to move along the general direction of the surface from your new position, which results in another collision-pushback, which further results in "sliding". Just make sure you check your new point through the collision detection scheme again. Collision response however, is a topic large enough that I think it would need its own tutorial (but not from me! :).

Other Things To Consider

I neglected various things (on purpose) that you may want to consider now that you know a method of doing collision detection.

Limiting The Potential Polygons - Obviously, the more polygons you have to check for collisions, the more calculations you have to do, and thus the slower your engine runs! But do you really need to check if you've collided with polygons that are ten rooms away?? Of course not. There are many ways to lower the amount of polygons you have to check. Suppose that parts of your world have bounding volumes. If the viewer doesn't pass a plane of the volume, obviously you don't have to check the contents of the volume. Extend that idea a bit, and what might we get? You guessed it! Octrees. There are some very cool speed-ups you can do with octree-enhanced collision detection, which can quickly eliminate large portions of the world that you would normally check. At its simplest, just keep in mind that if you don't collide with a particular octree node, you obviously haven't collided with any of its children.

Another thing to consider is the type of engine you're running. If you're doing something like a portal engine or a leaf-based bsp system with node-node connectivity, you can make use of the potentially visible set to only check against polygons that are in fact potentially visible and thus (not neccesarily) potentially collidable. That'll speed things up quite a bit. If you're running portals, you can check local sectors for example.

Viewer Bounding Volume - You may have noticed that I've been treating the viewer as just a point in space. That's definitely not the case in most applications. A simple fix is to slap a "bounding volume" around the viewer, for example as commonly used, a sphere. This way when you're checking if you've collided against a plane, just be sure to compensate for your sphere's radius. Everything else shouldn't need to be changed too much. This will prevent you from getting RIGHT UP to walls. All of the collision principles remain the same though.

Other Uses - Oh yes, you didn't do all of this work just for viewer / world collision detections. You can use this exact same system for anything else. For example, suppose you're generating lightmaps for your world and want to include shadows. You need to check if the light point actually reaches the destination lumel in world space, which means you need to check if that line is blocked by any other polygon in the data set. Sounds like collision detection to me! You'll find that it works exactly the same. For more on lightmaps, try here.

Closing

There you have it. Basic collision detection. I hope I explained it well and without any mistakes. This information should be accurate as I do have it up and running well, but once again, if you spot any errors then let me know. I'd also like to hear what you think of this tutorial and if you actually learned anything useful from it. Til next time... I leave you with a quote...

"... if work is interpreted to be a definite performance in a specified time according to a rigid rule, then I may be the worst of idlers."
- Nikola Tesla / The Forgotten Father Of Technology