|
3D Graphics on Mobile Devices - Part 1: Voxel Graphics by (08 August 2003) |
Return to The Archives |
Introduction
 |
|
In this short series of articles I plan to describe some of my recent work for Overloaded, a distributor and manufacturer of games for mobile devices. I am the game technology guy at Overloaded, so I'm focusing on reusable technology, like 3D engines, while working on actual titles, as we have to make money too. :) The articles will be a bit in the style of the portal column series, in the sense that I will present some technical details and some bits of source code, but I will also write a bit about my experiences with the subject and do some general rambling. As I'm writing this particular paragraph after completing the fourth article, I can now safely say that this style is not a goal but merely inevitable, apparently. In the first article, I will describe the platform and the technology used in the game 'Resistance'. Resistance is a fast-paced shoot'em up game with multiplayer support over bluetooth. In the second and third article, I will describe in-depth fixed point math and my current project, a regular 3D engine for a racing game currently under development. The fourth and final article will discuss the rasterizers used in the engine and the fixed point math in them. Note that although the 3D engines described in these articles are developed for the Symbian platform, the ideas presented are not just applicable on this OS. Software rendering techniques, engine design, low memory design and fixed point math are not simply things of the past, although the style of game coding is clearly shifting. Going further than the competition means going for optimal performance and quality, using all available means. Think about it. |
Symbian
 |
The platform that I am developing on is the Symbian OS, which powers the Nokia 7650 and 3650 phones, as well as the recently announced N-Gage gaming device. Earlier versions of this OS where used for the Psion organizers and the Nokia communicator. Phones equipped with this OS are powerful devices: The 7650 and 3650 come with 100Mhz ARM processors, while the Sony P800 is even faster, at 200Mhz. The Sony has a 320x200 12-bit TFT touch screen, the 7650/3650 have a resolution of 176x208 and lack the touch screen functionality. So, for regular graphics coding, we have the ultimate dream machine; it's small, powerful, and it has a linear framebuffer. Small drawbacks: The framebuffer is 12bit (444), and there is no floating point processor. There's a lot more to say about the OS and other hardware, but I am omitting this for now: The other hardware is not interesting for graphics coding, and the OS, well... Our strategy is to write a 'HAL' that takes care of the platform specifics. Somewhere in the past I coded in mode 13h, which was cool. Then Gates forced me to use Windows, so I switched to OpenPTC, which is basically mode 13h in a window. So when I start with a new OS / device, I first make it look like mode 13h. That's what the HAL does. There are some things in Symbian that you can't ignore though: The OS does not have a timer with decent accuracy (1/64th of a second is the best you'll get), and the compiler does not allow global variables and thus no static class members. |
The Engine
 |
| So now that the platform is clear, let's have a look at the requirements. Right now, there are not that many quality Symbian titles, and the market is small. This doesn't mean we can produce crap and still be the best, but it does mean we need to produce games fast. A typical project at Overloaded takes 6-8 weeks. In that time, you can do a 2D game, not a 3D game. In 3D, art becomes more complicated, and so does the rest of the game: AI, collision detection, controls. But I have my pride. :) So, I wanted to do an engine that looks 3D but is as easy to use as a 2D engine. A voxel engine is perfect for this. |
Voxels
 |
|
Strictly, what I call a 'voxel engine' is not really a 'volume pixel engine', but the height field renderer that Novalogic originally did for 'Comanche' is commonly referred to as 'voxel engine', so I'll call it that too. A voxel engine takes a height map and a texture, and renders it. Rendering is done in slices, front-to-back. Each subsequent slice is clipped against slices that have been drawn already. This way, a voxel engine draws the scene with zero overdraw. And, scene complexity barely affects the rendering speed. By the way, the finest game ever produced using a voxel engine is Appeal's Outcast, wich produces absolutely amazing graphics with it. A well-implemented voxel engine is very fast, especially at low resolutions. There are other advantages: The scenery can be modified in real-time, and collision detection works just as in 2D. There are disadvantages too: No overhanging geometry, since the dataset consists of a heightmap, and transformations are limited to translations and rotations about the y-axis (assuming y points up). But for us, voxels are perfect. Imagine a basic Pacman game. Now imagine the same Pacman game, but this time with the maze converted to a heightfield. You now have the same game, same game logic, but it looks much better. Since the game logic stays the same, the game can be churned out just as fast as the 2D version, and now that it is 3D, I can show off cool IOTD's, which is my primary raison d'Ítre, merci beaucoup. |
Technical Details
 |
|
Doing a basic voxel engine is quite easy. Each column on the screen is drawn by traversing a ray, starting at the camera position, passing through the viewplane. Since the heightmap is 2D, the rays are cast in 2D. At fixed intervals, we sample the heightmap. The heightsample is scaled to compensate for perspective. If the resulting value is above the pixels already drawn at that x-position, we draw the new visible part of the scenery and proceed with the ray. However, despite the fact that I wanted a simple-to-use engine, I didn't want a simple engine. This wasn't my first voxel engine either, so I learned a couple of lessons, and I wanted to raise the bar a bit. I had the following wishlist: The first requirement may seem obvious and easy at first, but I found that it's very easy to whip something up that looks like it has perspective, while it will never be possible to reverse engineer the '3D' formulas in it. The problem is that in a voxel engine, you're not transforming anything from objectspace to worldspace to cameraspace. You are drawing in screen space, and you want to know what should come at screen position (x,y). So, you want to reverse your projection. I usually use something like:
where Xc, Yc = horizontal centre of the frame buffer; Xworld, Yworld, Zworld = world coordinates; Xscreen, Yscreen = screen coordinates. When drawing a slice, we have the x coordinate in screenspace, and the y-coordinate of the base of the slice in screenspace. We also have the y-coordinate of the base of the slice in world space. That's enough information to work out Xworld and Zworld, and thus enough information to find out where we want to sample the height:
Those formulas essentially transform from screenspace to worldspace. The reverse formula's are used to determine the direction of the rays. I already mentioned that the rays are cast from the camera position through the near clipping plane towards the far clipping plane. We know the Z of the near clipping plane, but we want to calculate it's boundaries so that it fits exactly on the screen. The display is 176 x 208, so the near clipping plane has the following boundaries:
Interpolating from Xleft to Xright gives us the end coordinates for each of the 176 rays. Notice that the 'planes' are actually lines, as the rays are cast in 2D. Let's look at some ways to make the graphics more realistic: All this bilinear filtering may seem too slow to implement in a realtime engine, but it isn't. I've written a tutorial on that in some distant past, but I'll summarize the technique here: Bilinear filtering is done by sampling four pixels, multiplying each pixel by a weightfactor and summing the scaled colors. The four weightfactors are calculated as follows:
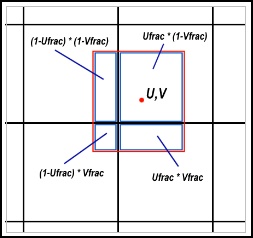 where
whereUfrac is the fractional part of the U coordinate where we want to sample; Vfrac is the fractional part of the V coordinate. Summed, the weightfactors equal one, the area of one pixel. Suppose we use 4 fractional bits for U and V. Then we have 256 possible combinations of U and V. So, we create a table with 256 entries, and we precalculate Ufrac * Vfrac. Each entry in the table contains four values: Ufrac * Vfrac, (1 - Ufrac) * Vfrac, (1 - Ufrac) * (1 - Vfrac) and Ufrac * (1 - Vfrac). So now, if we want to get the four weightfactors, all we have to do is take Vfrac, shift it by four, add Ufrac, and we can look up four weightfactors in the table. We have not performed a single multiplication yet, just a shift. Next, the weightfactors need to be used to scale colors. Normally, this is an expensive operation. We can use another trick though: Instead of using a random 16 or 32 bit texture, we use an oldskool 8-bit texture. And, we store the palette in 16 intensities. Now, when we have a weightfactor, we can lookup the scaled color in the palette. After looking up four colors this way, we can simply add them to get the final bilinear interpolated color or heightmap sample. |
Speeding Things Up
 |
|
There are a couple of ways to speed things up slightly. I'll discuss them briefly. First, I divided the rays in three parts. The first part is drawn with full quality: Bilinear interpolation of texture and height. The second part uses only height interpolation, the last part no interpolation at all. To render a larger depth range, I double the steps that I take when traversing the ray for each part. Next, I observed that the mainloop contains a nasty divide: The slice height needs to be scaled to compensate for perspective. To get this fast enough, I precalculate the scaled heights. Since the heightmap is 8 bit, this results in an array of slices * 256 values, which is quite acceptable. But the biggest gain came from a dirty trick: Interlacing. Since we're tracing a ray per column, it's very easy to omit one column. This will almost double the speed of the renderer. By alternating which columns we skip, we get an effect similar to the interlacing effect that some old monitors used (TV still uses it by the way). This is of course noticeable, but the speed gain is worth it. Besides, when the scene is not moving, the renderer 'catches up' and you get to see the full detail. We added an option to blur the drawn columns with the columns from the previous frame. This results in a cool motion blur, and it's still faster than drawing all columns. |
Sprites
 |
|
The game that we used this engine for, 'Resistance', uses the engine in it's simplest form. All the action occurs above the peaks of the mountains. That way, we don't have to take care of sprites that are obscured by mountains, all sprites are simply drawn after the renderer did it's job. The perfect reverse projection formula's helped a great deal to get the sprites at the correct position. A logical extension to the renderer is code to handle sprites in a more generic way. We would need that functionality for the Pacman example that I used in the beginning; Pacman will be frequently behind a wall, obviously. This is not as easy as it looks at first: The heightfield is rendered front-to-back, which is only possible because there's no overdraw. The only way to blend in sprites in this routine is by making sprite drawing overdraw free too. This is very hard, so we need a trick. Suppose we attach each sprite to a slice that matches it's depth. Then, after that slice is rendered, we store the heights of the drawn slices, so that we can clip the sprite against those heights. Once the entire heightfield is rendered, the sprites can be rendered back-to-front. Adding polygons is also possible, but this requires a z-buffer, since a polygon can cover a range of depths. I found adding a z-buffer too slow, so I skipped it for the moment. |
Demo Application
 |
I have enclosed the demo version of 'Resistance', so that you can see the engine in action. Some notes about the demo:
Download: resistance.zip (609k)  |
Conclusion
 |
|
We now have a good looking engine that is as easy to use as a 2D engine. And it's very fast too. Some extensions are needed to make it even more useful though. On mobile devices, it's often neccessary to brush up your knowledge of oldskool techniques. Voxels may not be the latest thing, but they surely kick ass on a mobile phone. And coding it is quite a ride. :) By the way, did I mention that the algorithm I just described had to be implemented without floating point code? I think I did. :) The next article will describe the polygon engine that I'm working on now. Until then: Have fun. - Jacco Bikker, a.k.a. "The Phantom" |
|
Article Series:
|