|
Light Mapping - Theory and Implementation by (21 July 2003) |
Return to The Archives |
Introduction
 |
|
Ever since the days of Quake, developers have extensively used light mapping as
the closest they can get to realistic lighting. (Nowadays true real-time
Per-Pixel-Lighting is slowly replacing light maps). In this article I am covering a simple but quick light mapper that we developed in 2001 for use in our internal projects at Dhruva Interactive. The method is not as precise as radiosity based techniques, but nevertheless produces results that are effective and usable. This article will be useful for people who haven�t got light maps into their engine / level yet, and are looking for relative resources. |
Overview
 |
|
This document explains / demonstrates the process of creating light maps for use
in games or any graphics application. Objectives The goal of this document is to explain the process of creating light maps. It describes how light map lumels are calculated and how the final pixel color is determined. However, this document does not cover any of the latest �per-pixel� techniques that are possible with the new generation graphics chipsets. Assumptions It is assumed that the reader has in depth knowledge of 3D game programming and the essentials of 3D graphics, especially lighting, materials, 3D geometry, polygons, plane, textures, texture co-ordinates, etc. Also, this document explains only the process of light map evaluation or generation � it does not explain how light map texture co-ordinates are calculated. If you do not have light map texture co-ordinates in your mesh yet, then, I�ve got a simple method to test the light map generation. Click here to read more on this. If you are really eager to know the results of a light map based lighting technique before you get on with this article, then click here to go to the demo section, where you can download an interactive demo. |
Lighting Basics
 |
You've seen games which look pretty close to real life ambience (I mean, only look wise).
The reason for that, is the use of lights. If the game was not "lit", then, it would look less than ordinary.
It is the lighting, which makes the player, look at the game again and again.
Take a look at what difference, lighting makes: World with light-map lighting. The white rhombus type object (on the right hand side) represents a point light source.  World without any lighting. The results are impressive, aren't they? Now that you�ve seen the results, let�s take a look at the different types lighting in practice (as far as the "static world" is concerned). 1. Vertex lighting: 2. Per-pixel lighting (Real time): This document does not cover the per-pixel lighting methods that are in practice today, i.e., the effects that are achievable on current generation of graphics cards, like NVIDIA GEForce 3/4, ATI Radeon 8500/9700 and later. 3. Per-pixel lighting (light map):
|
Per-pixel Lighting Using Lightmaps
 |
A Simple Lightmap Based Lighting Technique
 |
Now let�s get on with the actual process of light mapping.
The complete process of calculating light maps is split into three parts. They are:
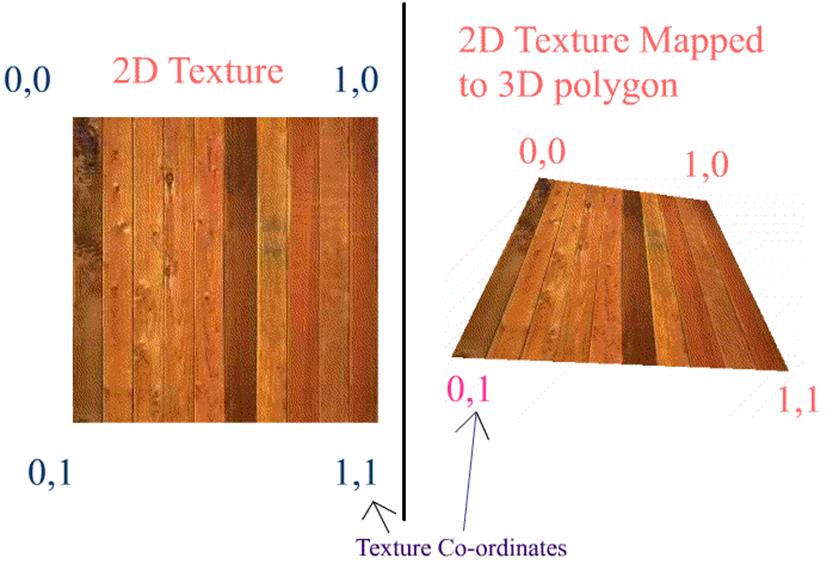
a. Calculating / retrieving light map texture co-ordinates: This is the very first and basic process. It involves assigning each polygon to a specific area of the light map. This topic in itself is a candidate for a lengthy article. Hence, I'm going to skip this topic and jump to the next one. However, if you want links to articles that explain this, then, I've provided some in the links section, at the very end of this article. Also, this is one of the most important processes, since it determines the efficiency of using texture space. This can either be done in an automated process or can be done manually in editing tools such as 3DS Max� or Maya�. However, if you want a quick way to generate a world to test light maps, then you can do this:
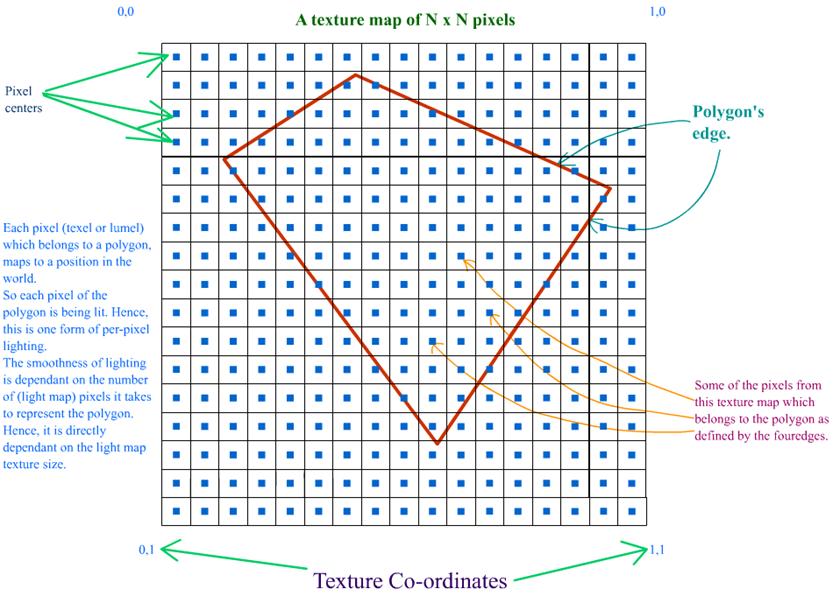
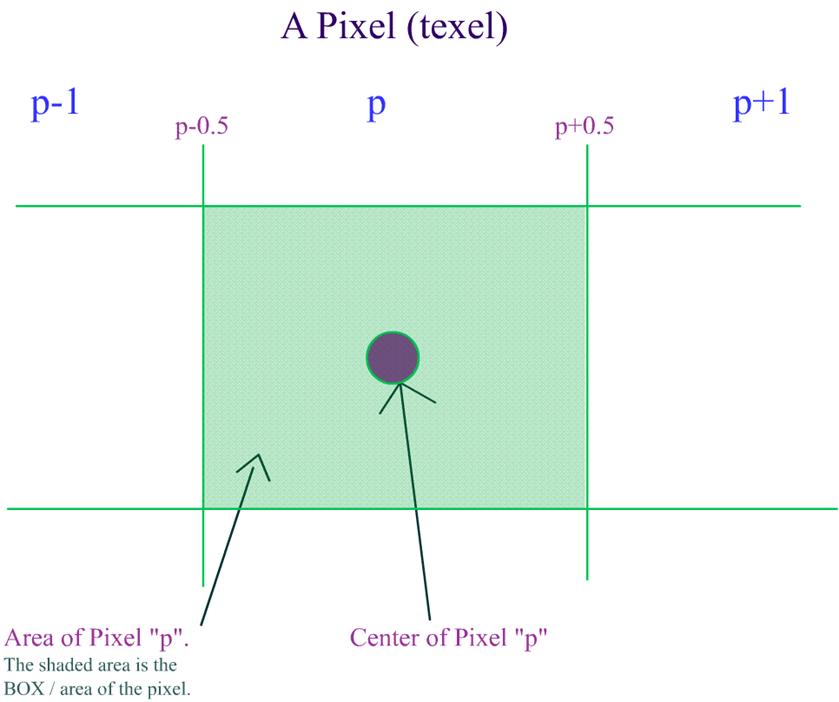
b. Calculating the world position and normal for every pixel in every light map: This is the pre-processing stage of the light map calculation. As you know, each pixel in the light map will map to a position in the world. This is exactly what we need to calculate. As long as the world geometry and the light map texture sizes doesn�t change, this data is static, i.e. it can be calculated once and reused. This is how it is done. Now consider a triangle like this. Why we have only 2D components for vertex position in the below triangle will be explained in later paragraphs. 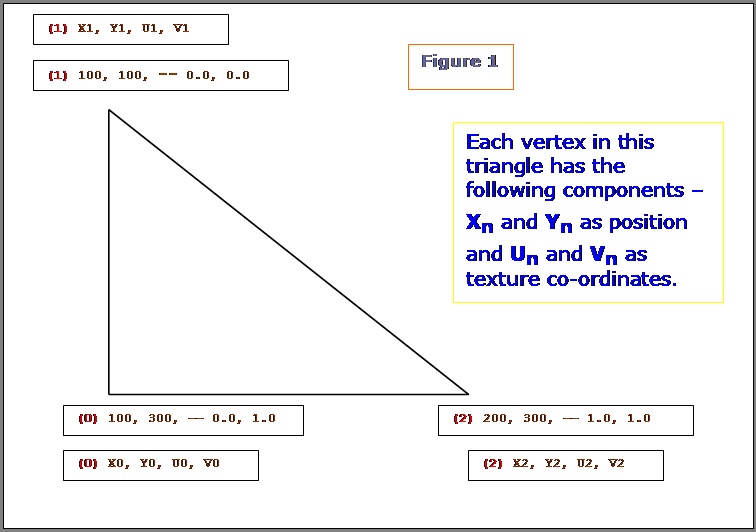 Let�s see what are all the know factors here: What do we need to calculate here: Given a texture co-ordinate value (on or within the 2D triangle), retrieve the 2D position on or within the 2D triangle. We have to do it for every pixel of the light map that this polygon owns. (Remember, a pixel from a light map can belong to one and only one triangle / polygon.) Let's see how we can achieve this. NOTE: In the following few paragraphs, I�m using certain equations, illustrations and quotes from Chris Hecker�s article on Perspective Texture Mapping. Please refer to the above said article for more information. 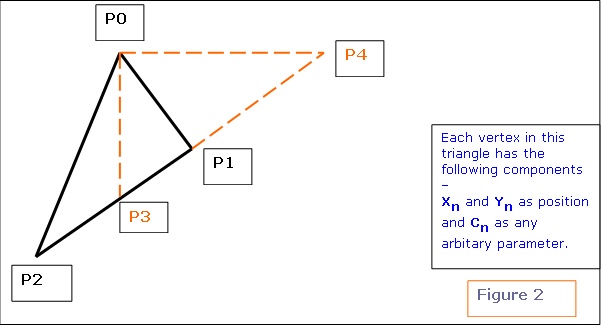 Consider triangle P0, P1, P2 in the above diagram. Each vertex has a screen space (2D SPACE) associated with it i.e. (X, Y). But in addition, there is an arbitrary parameter, C, which is, color for Gouraud Shading, or 1/Z, u/z or v/z for perspective texture mapping. Hence �C� is any parameter we can linearly interpolate over the surface of the two-dimensional triangle. For the derivation, two points P3 and P4 are constructed as shown in the above diagram. Therefore,
We know that y4 = y0 and x3 = x0. Click here to see the derivation as to how we arrived at equation 1 and 2 mentioned below. For the triangle, we get the following two equations:  The above two equations tell how much of variable �C� varies w.r.t X and Y. i.e. given a position (x, y) we can calculate �C� for that position. For our lightmap solution, we need just the opposite. We know the texture co-ordinates (i.e. �C�) and we need to retrieve the position. I will be using the formulas as mentioned below. These are directly inherited from the above two equations. (Please refer to figure 1 for the variable names)
Now get uv position relative to the first vertex�s light map texture co-ordinate.
uv is the pointer to the texture co-ordinate for which the �world-position� has to be computed. U0 and V0 are the light map texture co-ordinates for the first vertex. Let pos be the pointer to final position.
Now we have the 2D position corresponding to the triangle and the UV coordinate. Let's look at the figure 1 as an example, and try to retrieve the position for a given UV co-ordinate: Let the UV co-ordinate for which the Position has to be calculated be {0.5, 1.0 } We definitely know that co-ordinates {0.5, 1.0 } fall well within (or on) the triangle. We get the following values:
Hence the position is:
You can change the winding order and try � you'll get the same result. Only the dxdu, dxdv, dydu, dydv, and duv values will change. Now, we've retrieved the 2D position w.r.t a UV co-ordinate. But finally, we need a 3D position to do any 3D calculations. How do we do this? Here's the plane equation to the rescue. We know that a plane is represented by the equation: Ax+By+Cz+D = 0. Every polygon / triangle has a plane equation associated with it. Also, we can project any triangle/polygon along two of it's major axis. i.e. we are projecting a 3D triangle to 2D, by ignoring one of it�s axis. This is required, because a texture is 2D whereas a triangle is in 3D space. Which axis � X, Y or Z to ignore? How we choose the axis to ignore is, given the plane normal, choose the two axis that are most aligned to the plane normal. If a, b, c (analogous to x, y, z axis) represent the plane normal, then, find out the maximum of the absolute of these three values, and ignore that axis. Ex. If plane normal is (0, 1, 0), then, we would choose XZ axis and ignore the Y component. If plane normal is (0, -1, 0), then also, we would choose XZ axis. Now we'll refer back to figure 1. If the plane normal for the given triangle in figure 1 was (0, 1, 0), then the (Xn, Yn) values specified for each vertex in the figure, would actually be Xn and Zn. , I've used (Xn, Yn) in the figure to keep the derivation consistent. Remember, the triangle is still in 3D, but we�re converting it to 2D by ignoring one component. Look at equation 3. Now, we've the world position of the lumel in 2D co-ordinates. We've to convert it to 3D. So, use the plane equation. Depending on which axis we�ve projected the triangle, we have to use the appropriate equation. For example: The plane normal was (0.123, 0.824, 0.34). According to what I�ve mentioned above, we ignore the Y � component. Hence, when we get the 2D position of the lumel, it will be the X and Z components. We need to calculate the Y component. We have Ax+By+Cz+D = 0. By = -(Ax+Cz+D) y = -(Ax+Cz+D) / B. Thus we have the Y component. Similarly, we can calculate the missing component for other projections also. First, let's look at the Lumel structure.
This structure is used for every pixel in every light map. Ex. If the dimensions of a light map are 64x64, then, the memory required to hold the lumel info Would be: size of each Lumel structure = 40 bytes. Total size = (64 * 64 * 40) bytes = 163840 Bytes = 160 Kbytes. This is just a test case. You CAN reduce the memory foot print. "LegalPosition" member of the Lumel structure, will hold information whether the particular pixel belongs to any polygon or not. The structure for a vertex displaying a light map would look something like this.
The structure for a polygon displaying a light map would look something like this.
Here�s the pseudocode for a function called BuildLumelInfo() that actually fills in the world position for every pixel in the light map:
The function to build the lumel information is as follows: Remember, as long as the geometry, light map texture co-ordinates and light map texture sizes are constant, this function can be called only once and re-used again and again. This way, if you change a property for a light, then, you don't have to build the whole data base again. All you have to call is the function BuildLightMaps. BuildLumelInfoForAllLightmaps() should be called before BuildLightMaps().
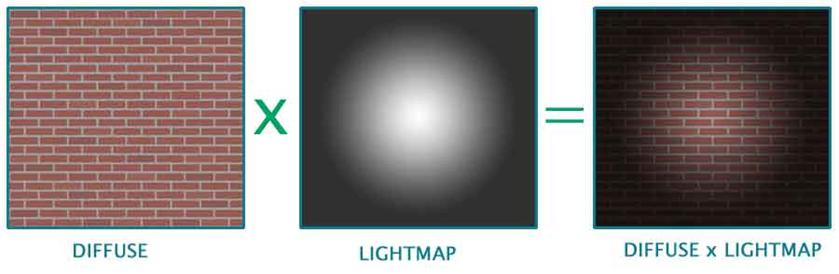
c. Calculating the final color for every pixel: This is the last process involved in the calculation of light maps. Here we fill out the actual pixel values in every light map. I'll first give the pseudo code here which calculates the color for every pixel in the light map.
As you can see, the pseudo code explains itself pretty well. It's the basic light calculation. I won�t spend too much time there. Let's look at the procedure which starts the process of calculating colors for all the light maps.
Lets look closely at what the two functions BlurThisMap and FillAllIllegalPixelsForThisLightMap do. No matter whatever we do, if you�ve NOT turned on any filtering, then, "pixels" can be seen in the final rendered image. This is very unrealistic and can easily annoy the player / viewer. Hence, we try to smoothen out the "pixels". You can use any filter you want for smoothing. I�m using a BOX filter in my code. This is exactly what my BlurThisMap does.
Actually, if you�ve turned on Bi-Linear filtering in your game, then, the effect of "pixels" are reduced. But, still we smoothen out the map, to make the final image appear really smooth. If the final result (in the game) looks good without blurring the light map texture, then, you may skip the BlurThisMap procedure. There's another problem if we use bi-linear filtering. It's the "bleeding" problem. When bi-linear filtering is turned on in your game, then, whenever a pixel is chosen, the final color will not be the color from the pixel alone, but, the average of the pixels around it. (average of how many pixels - depends on the kind of filtering used.) As you know, some of the pixels in our texture map will be illegal. It means, that particular pixel belongs to no polygon. Usually, the color of any illegal pixel will be zero, since no color calculation is being done for that pixel. So, while rendering, whenever a pixel is chosen, the average of the color around that pixel will be considered. In this process, even the "illegal" pixels may be chosen. This is why "bleeding" happens. If we're using bi-linear or tri-linear filtering (which I bet we would be) in ourgame, then, we somehow got to get rid of the illegal pixels. Actually, we can't get rid of them. What we can do is fill every illegal pixel with a color from the closest "legal pixel". This way, during filtering, it is assured that the closest and most appropriate color is chosen. This way, most of the "bleeding" problems will be solved. This is what the procedure FillAllIllegalPixelsForThisLightMap does. One way of solving "bleeding" problem, without having to fill out illegal pixels, is to set the color of all the illegal pixels to ambient color. Even though this gives decent results and is also very inexpensive, it's not the correct way of doing it. Maybe, you can consider this method for real-time light map generation. Take a look at the figure below:  Bleeding due to bi-linear filtering being turned on.  No bleeding even if bi-linear filtering is turned on. Showing the lightmap: Now that you�ve taken so much time to calculate the light maps, it�s �display time�. Here�s the code for DirectX 8.1:
|
Winding up...
 |
|
As I have mentioned above, you have to look into Chris Hecker�s article for more explanation on some of the equations I have used. Some more illustration of using light maps: To assert the effectiveness of using light maps, a scene has been rendered with different properties / effects. Click on each of the link below to see the images: Where can you go from here?
Conclusion: With the arrival of new monster graphics cards, lighting using lightmaps may become extinct. This article does not provide you any cutting edge technology for today�s hardware, but it does provide some basic but useful information on the process of creating light maps. Demo: An interactive demo has been included with this article where you can see the practical results of this article. I suggest that you download the demo and have a look at the results your self. After you have downloaded and unzipped all the files, look into the readme.txt file for more info. Feel free to play around with the lights. In the demo, you can add and delete static and dynamic lights, change the light properties and build light maps on the fly - and see the results. It's a very good example for using light maps. Click here to download the demo (~2.1 MB). (* Editor's note: source code is not included with this demo.) Credits and Acknowledgements: Please look at Chris Hecker�s article on Perspective Texture Mapping at: http://www.d6.com/users/checker I would also like to thank my company for permitting me to publish this article. I also acknowledge the contributions of all my team members. Links: Click here for some info on light map co-ordinate generation. http://www.flipcode.com/cgi-bin/msg.cgi?showThread=06June2000-LightmapStorage&forum=askmid&id=-1 Some more links to articles or docs about light maps: http://polygone.flipcode.com/ http://www.flipcode.com/cgi-bin/knowledge.cgi?showunit=79 http://www.flipcode.com/tutorials/tut_lightmaps.shtml Some Information about the author: Keshav Channa is the team lead - Engineering, at Dhruva Interactive, India's pioneer in games development. He was part of the team which ported the Infogrames title Mission: Impossible to the PC and has been an integral part of Dhruva's in-house R&D efforts. Previous articles include �Geometry Skinning / Blending and Vertex Lighting� published on flipcode. He is currently working on a multiplayer game for the PC. You can see his work at the Portfolio section at www.dhruva.com Keshav can be contacted at kbc at dhruva dot com. |
Derivation
 |
NOTE: The following section is extracted from Chris Hecker�s article on Perspective Texture Mapping and the derivation elaborated further.   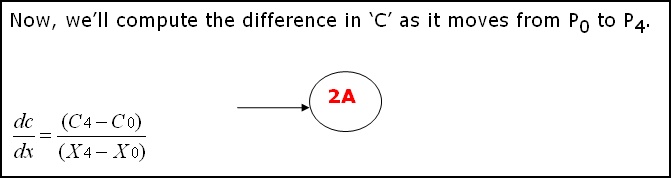 (The equations are from Chris Hecker�s article on Perspective Texture Mapping. The only thing I�m doing from here onwards, is elaborating the derivation.) The derivation is very simple and involves plain substitution and some re-ordering.     |
|
|