|
3D Geometry Primer: Chapter 1 - Issue 04 - Vector Bases by (04 September 2000) |
Return to The Archives |
Vector Bases: A Way To Store Vectors
 |
| We already know how to play around with vectors on 2D paper. We can draw them and make constructions. We still need to transform this to "number math" if we want to use this on a computer. |
(I) Vector Bases And Component Values
 |
|
a) 2D SITUATION: In the previous chapter we saw that it's possible to decompose vectors and to make linear combinations. If you look closer, you can see that it should be possible to create each free 2D vector with a linear combination of those same 2 vectors U and V. For each vector you decompose to the directions of U and V, you can find an r and s for which the linear combination r*U+s*V equals that vector.  You can do that with almost every pair of vectors like U and V. A pair of vectors you use to create all other vectors in your space, is called a base. We call both vectors the base vectors, and normally we call those base vectors I and J. We can give that base itself a name too: e.g. B. As you can see we use bold italic capitals for that. If you want to show B with its elements, you can write B{I, J}. We see that I and J are the 2 base vectors inside B. Now we have a base of our 2D space, we can write each vector V in that space as a linear combination of the base vectors: V = x*I + y*J. You can see that we've used x and y now. These are just the letters they use. (I've also changed the colors somewhat. This is because I want to use the "RGB-colors" for the "XYZ-stuff" now: Red is X, Green is Y, and Blue is Z. In that way, all images should have a "standard look" and be more comprehensible.) 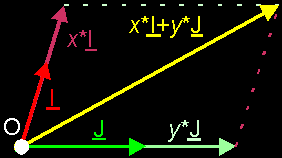 If you have a fixed base B, then for each vector V, the values x and y are unique. This means that there are no 2 vectors with the same values x and y AND for one vector V you can find only one x value and one y value. This gives us the idea to connect the pair (x, y) to the vector V. When you know (x, y), you know V and when you know V, you can find (x, y). We call (x, y) the component values of the vector V. This is much like cartesian coordinates of a point. Because the values (x, y) offer useful information about the vector, we often write the vector together with its component values: V(x, y) Where does the name component values come from? Well, it are the values you need to multiply the base vectors with, to become the vector components of V. The vector components of V are the vectors x*I and y*J you need to add together to get V itself. It are the vectors you get when you decompose V to the directions of I and J You remember that I said "You can do that with almost every pair of vectors like U and V"? This is because there's a giant condition to a set of base vectors: the set needs to be linear independent (1). In 2D, this means that it may not be possible to write one vector as a scalar product of the other vector. Or... both vectors may not have the same direction, may not be on the same line. Also, you cannot use the null vector O as a base vector, because if you add 536 times O to a vector, you still have that same vector. So you can't construct vectors with the null vector. Also, the null vector is linear dependent with any other vector: you can write O as O = 0*V (null times V) 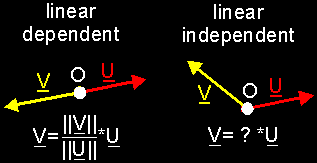 In short: A base B of a 2D space consists of 2 linear independent base vectors I and J. You can write each vector V as a linear combination of the base vectors: V = x*I + y*J. x*I and y*J are the vector components of V and x and y are the component values. In that way, we connect to the vector V a couple of values (x, y) Exercises: OK, I'll help you to understand this with 2 exercises. You will find the sollutions at the end of this issue ... 1. Write down the component values of vectors A to E (I and J are your base vectors :) 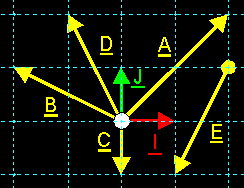 2. Draw an orthonormal 2D base, and draw the following vectors: A(0, 2); B(–2, 2); C(–1, 0); D(–2, –1) and E(2, –1) b) 3D SITUATION: In 3D space, we need to add an extra vector to our base. Otherwise, we wouldn't be able to create all vectors in space. We would only be able to create the vectors on the plane spanned between I and J. So, we add an extra base vector: K. Our base is now B{I, J, K}. If K is not part of that plane, then we can reach all vectors again. Each vector V can now be written as a linear combination of the vectors I, J and K: V = x*I + y*J + z*K. As you can see, we've added the component value z, and again those 3 values x, y and z are unique. We can connect each vector V with component values (x, y, z) now. 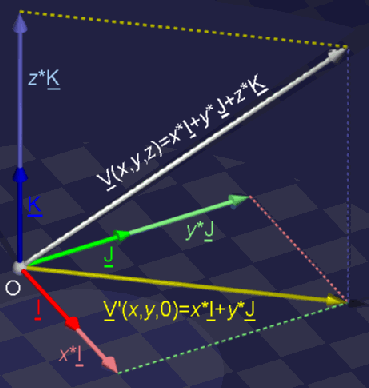 What does the condition "the base needs to be linear independent" mean? It means that you may not be able to write 1 base vector as a linear combination of the others. This means that the 3 vectors may not lay on the same plane. e.g. in the last image, vectors I, J and V' are linear dependent; I, J and K are linear independent. c) nD SITUATION: In nD space, you need n base vectors to reach all vectors in your space. Of course, all those vectors need to be linear independent to each other. You may not be able to write 1 base vector as a linear combination of the (n-1) others. In nD space, we call the base vectors I[1], I[2], ..., I[n]. The component values are x[1], x[2], ..., x[n]. Thus, each vector V can be written as V = x[1]*I[1] + x[2]*I[2] + ... + x[n]*I[n] and so we can connect V with its component values (x[1], x[2], ..., x[n]). |
(II) Orthogonal And Orthonormal Bases
 |
Until now, we used very irregular bases. There weren't special
conditions, except for the linear independency of the base vectors.  I'll tell you now that if you should use such a irregular base, you will have a lot of troubles incase measuring angles and distances. Orthogonal projections and decompositions of vectors will be very difficult. It is possible too, but it just ask to much efforts. Thus we need a perfect base, one that can do all that stuff without much of trouble. One step to the perfect base is when you pick all base vectors perpendicular to each other. Then you have a orthogonal base. 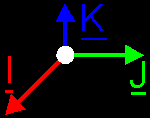 You can do things somewhat easier already, but it ain't magic (or it *is*. It all depends on what you see as magic: the simplicity or the difficulty of math. I prefer the first one) The ideal base is when all base vectors are perpendicular to each other *and* when all base vectors have magnitude 1. Then you talk about an orthonormal base. 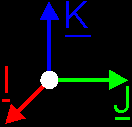 This is what you use best in your engine if you don't want to have much math troubles. Of course, for weird effects you could use a irregular base and treat it like it's a orthonormal one. But that's for some other time. Also, there's more than one possible orthogonal or orthonormal base in your space. In short: in nD situations: irregular bases: n base vectors, linear independent. No further conditions orthogonal bases: same as irregular bases PLUS base vectors stand perpendicular to each other. orthonormal bases: same as orthogonal bases PLUS all base vectors have magnitude 1 |
(III) Sequence Of Base Vectors
 |
|
There isn't a lot to tell about the sequence of base vectors, except that it
does matter. What I mean is this... If you swap 2 base vectors, then you have
a different base. e.g. in 3D: if you have a base
B{I,J,K} and you would swap the vectors
I and J, then you would have the base
B'{J,I,K}. Is this important? Very! Take a vector V with component values (x,y,z) (i.e. V(x,y,z)=x*I+y*J+ z*K), and apply these values on the base B'{J, I, K}. Then you get the vector x*J+y*I+z*K. And that vector definitely differs from the original V. Especially the cross product suffers from it. The moment you need one little cross product and *bwaff*, you get in serious troubles if you don't respect the sequence of your base. For other basic operations, it doesn't really matters, but there are only a few cases in which you don't need cross products. I have to admit that I didn't realized it myself, until I learned the next thing about 3D bases: there's a difference between your lefthand and your righthand. But that's something for next week! |
(IV) Important Properties Of An Orthonormal Base
 |
|
Before we say goodnight, I want you to check out the following things about orthonormal
bases. These are very important identities about base vectors, and you have to
know them well. Each time you use a orthonormal base, you have to realize
immediately that these things can be used. And each time you use the following stuff,
you have to check for yourself if you're working in a orthonormal base. Say, we have a orthonormal base B{I,J,K} a) MAGNITUDES ||I||=||J||=||K||=1 Of course this is true. It's part of the definition of a orthonormal base b) DOT PRODUCT I·J = J·I = 0 J·K = K·J = 0 K·I = I·K = 0 This is true because all base vectors are perpendicular to each other (orthonormal base) I·I = J·J = K·K = 1 This is also true because U·U = U² = ||U||² for each vector U, and thus also for I, J and K. c) CROSS PRODUCT I×J = K J×K = I K×I = J Why this is will be explained next week, but you should already notice: 1. the similarity between the orthogonality of I, J, K and the cross product 2. the cyclic permutation between each rule: I becomes J, J becomes K and K becomes I again. 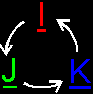 Next week, more on this... Regards, Bramz |
Solutions
 |
|
1. A(2, 2) = 2*I + 2*J B(–2, 1) = –2*I + J C(0, –1) = –J D(–1, 2) = –I + 2*J E(–1, –2) = –I – 2*J (move E to the origin, if you don't see this) 2. 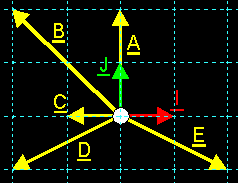
|
Remarks
 |
| (1) A set of vectors is called linear dependent if it is possible to write a least 1 vector (of that set) as a linear combination of the other vectors (of that set). A set of vectors is called linear independent if this isn't possible. (e.g. 2 vectors on the same line are linear dependent, 3 vectors on the same plane are linear dependent, 2 vectors perpendicular to each other are linear INdependent, ...) |